¿Eres exigente con los pequeños detalles? Bueno, si eres fotógrafo, es mejor que lo seas. Descubrir la regla de los tercios es un gran hito para cualquier fotógrafo. De repente, te das cuenta de que todo lo que habías hecho antes era centrar el sujeto justo en el medio del encuadre, porque ahí es donde se encuentra la cuadrícula de enfoque de la cámara. Tiene sentido, ¿verdad? La regla de los tercios lo llevó a nuevas alturas en su viaje fotográfico, moviendo su sujeto hacia un lado u otro en su marco, hacia arriba o hacia abajo. Pero, ¿no se ven algunas de estas fotos un poco abarrotadas al estar tan cerca de ambos lados del marco? Seguro que funciona en algunos casos, pero ¿y si aún hubiera otra regla que pudieras incorporar a tu repertorio fotográfico?
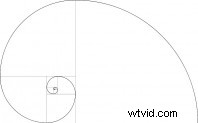
Ingrese la relación de Fibonacci...
También conocida como la Proporción Dorada, Phi o Divina, esta ley se hizo famosa por Leonardo Fibonacci alrededor del año 1200 d.C. Se dio cuenta de que había una proporción absoluta que aparecía a menudo en la naturaleza, una especie de diseño que es universalmente eficiente en los seres vivos y agradable al ojo humano. De ahí el apodo de “divina proporción”.
Desde el Renacimiento, los artistas y arquitectos han diseñado su trabajo para aproximarse a esta proporción de 1:1.618. Se encuentra por todo el Partenón, en obras de arte famosas como la Mona Lisa y la Última Cena, y todavía se usa en la actualidad. La proporción divina ha sido utilizada por empresas como Apple para diseñar productos, se dice que Twitter la ha utilizado para crear su nueva página de perfil y ha sido utilizada por las principales empresas de todo el mundo para diseñar logotipos. No se habla en la mayoría de los círculos de fotografía porque es un método de composición algo avanzado y puede ser confuso para mucha gente. Es mucho más fácil hablar simplemente de la "regla de los tercios" porque es exacta, precisa y fácil de seguir.
Esta relación se puede utilizar de muchas maneras para componer una fotografía. Lightroom 3 incluso tiene una opción de superposición de proporción áurea cuando vas a recortar la imagen. De esta manera, puede alinear una cuadrícula de la proporción áurea para que coincida con líneas o puntos de interés en su fotografía. En este punto, usted puede estar bastante confundido. Si es así, tómese unos minutos para ver uno (o todos) de estos videos que buscan explicar esta proporción.
Video 1:Naturaleza Número:1.618
Video 2:Naturaleza por Números
Vídeo 3:Proporción áurea
Ok, con suerte eso hizo las cosas un poco más claras. A estas alturas ya deberías saber que esto NO es una teoría de la conspiración o matemáticas difusas. Este es un aspecto real de la composición que ha sido utilizado por artistas y arquitectos históricos famosos y compañías Fortune 500. Cuando se aplica a la fotografía, esta relación puede producir composiciones estéticamente agradables que pueden ser imanes para el subconsciente humano. Cuando toma el punto óptimo de la relación de Fibonaci y lo recrea cuatro veces en una cuadrícula, obtiene lo que parece ser una cuadrícula de regla de tercios. Sin embargo, después de una inspección más cercana, verá que esta cuadrícula no es una división exacta del marco en tres partes. En lugar de una cuadrícula de 3 piezas que va 1+1+1=marco, obtienes una cuadrícula que va 1+.618+1=marco. Aquí hay algunos ejemplos de una cuadrícula Phi colocada sobre algunas imágenes en las que la he usado en el pasado...
En el ejemplo anterior, coloqué el ojo ligeramente más dominante del caballo en una de las intersecciones de Phi. Considere que si hubiera colocado una cuadrícula de regla de tercios sobre esta foto y alineado el ojo con eso, la cabeza estaría abarrotando el lado izquierdo del marco. En esta foto, la cabeza no está en el centro, no se amontona a ningún lado. Es justo, ¿estás de acuerdo? Echemos un vistazo a otro…
Este es ligeramente diferente. Si eres un VERDADERO estricto con los detalles, es posible que hayas notado que hay una ligera diferencia entre las líneas que se cruzan del gráfico Phi y el punto óptimo de Phi. En esta imagen, me aseguré de alinear la cabeza de mi sujeto dentro de la espiral y coloqué el ojo izquierdo aproximadamente sobre el punto óptimo. Bien, sigamos…
En esta fotografía, de Cayo Hueso, alineé el horizonte con la línea superior de la cuadrícula Phi. En mi opinión, cuando alineas el horizonte con una cuadrícula de regla de tercios, la separación es demasiado... obvia. Creo que dejaría demasiado de lo que no es el sujeto en la imagen. En esta foto, el cielo y las nubes son el complemento perfecto para lo que estoy tratando de transmitir en la foto:la iglesia abajo a la derecha y la famosa calle Duval a la izquierda. Pero con más cielo del que ya está presente en la foto, el espectador podría pensar que el cielo es en realidad el sujeto. Aquí hay uno más...
En este ejemplo, utilicé varias líneas en la cuadrícula Phi para mi composición final. Alineé las puertas con ambas líneas verticales, así como con la línea horizontal inferior. Esto proporcionó una cantidad perfecta de techo para guiar a los espectadores hacia la puerta. Aquí hay algunos ejemplos más sin la cuadrícula. Vea si puede imaginar la cuadrícula sobre las imágenes y determinar por qué la imagen se compuso de la forma en que se compuso.
Conclusión
Con suerte, este artículo ha arrojado algo de luz sobre un tema un tanto misterioso en el mundo de la fotografía. La proporción de Fibonacci es una herramienta poderosa para componer tus fotografías, y no debe descartarse como una diferencia menor con la regla de los tercios. Si bien las cuadrículas se ven similares, usar Phi a veces puede significar la diferencia entre una foto que simplemente hace clic y una que no se siente bien. Ciertamente no estoy diciendo que la regla de los tercios no tenga cabida en la fotografía, pero Phi es un método muy superior, mucho más inteligente e históricamente probado para componer una escena.
Si desea comenzar a incorporar esta poderosa herramienta de composición en su fotografía, ¡está de suerte! He incluido una superposición PNG tanto de la Espiral de Fibonacci como de la Cuadrícula de Fibonacci. Simplemente haga clic en este enlace de descarga para comenzar a usarlos. Estas superposiciones son para usar en Photoshop. Simplemente colóquelos en el archivo en el que está trabajando, luego escálelos al tamaño correcto de la imagen.